О моей учёбе на математическом факультете ИВГУ.
Учёба идёт очень успешно. Пока всё для меня просто. Интересующиеся могут посмотреть программу учебного курса по алгебре
Яцкин Н. И. Линейная алгебра: Теоремы и алгоритмы. Иваново, 2008.
Всё это я довольно прочно усвоил. Не думаю, что всё это тавтология, хотя иногда так и кажется. Довольно интересный философский смысл во всех этих теоремах алгебры всё же присутствует.
По аналитической геометрии на последней лекции было очень мало нового для меня. Применение критериев коллинеарности и компланарности векторов в решении геометрических задач подробно рассмотрено в учебнике А. Д. Кутасов, Т. С. Пиголкина, В. И. Чехлов, Т. Х. Яковлева «Пособие по математике для поступающих в ВУЗы», Москва, «Наука», 1985. Я решил очень много конкурсных задач из этого учебника, когда готовился к вступительным экзаменам в МГУ на мехмат. О том, как вычислять векторное и смешанное произведение векторов, я тоже давно знаю. Хотя надо отметить, что меня научили очень лёгкому новому способу решения задачи нахождения координат вектора, перпендикулярного двум другим векторам с заданными координатами, имеющего заданную длину и составляющего, например, тупой угол с одной из осей координат: этот вектор будет коллинеарен векторному произведению этих двух векторов с заданными координатами, следовательно, его координаты будут пропорциональны координатам векторного произведения этих векторов. Решение этой задачи значительно усложнилось бы, если бы вместо этого уравнения надо было записывать два уравнения равенства нулю скалярных произведений этого вектора на каждый другой. И я очень был удивлён тем, что такая задача вызвала у студентов затруднение. Жанна Александровна также была удивлена.
А вот на математическом анализе меня действительно научили новому, чего я раньше не умел.
Я, как ни пытался, так и не смог догадаться о том, как доказать методом математической индукции, не пользуясь замечательным пределом (числом e) и формулой бинома Ньютона эту формулу:
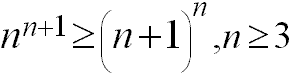
Или очень тупой я, или думать мне было лень. А доказывается эта формула очень просто:

Но зато потом я наверстал упущенное и научился решать все подобные задачи. На контрольной работе только двое из группы: я и ещё один человек успешно справились с решением двух подобных задач, которые были предложены.
Если уж в первый месяц обучения я научился очень многому новому, чего раньше не умел, то в дальнейшем научусь ещё очень и очень многому, следовательно, время не будет потрачено зря.
О том, как доказать равномощность множества всех точек отрезка [a, b] и интервала (a, b) я догадался много лет назад, когда изучал "Курс математического анализа2 Л. Д. Кудрявцева и выполнял предложенное там упражнение.
Но на лекции нам сказали, что множество точек числовой прямой и множество точек плоскости являются равномощными, но не представили доказательств этого факта. Мне очень захотелось узнать, как это доказать, и я спросил преподавателя об этом. Галина Александровна рекомендовала книгу Хаусдорфа «Теория множеств». К сожалению, в читальном зале не оказалось этой книги.
Друзей по интересам пока у меня нет, практически ни с кем не общаюсь. Правда, сегодня, 4 ноября в Иваново из Москвы приезжал Игорь, представитель РТД (Российского трансгуманистического движения), и мы много беседовали с ним о различных философских вопросах. Меня приглашают в Москву, принять участие и выступить на семинаре по трансгуманизму, но я не могу и не хочу пропускать занятия. В Иванове семинары по трансгуманизму не проводятся. По словам Игоря, в Иванове существует только общество последователей философа Владимира Соловьёва.
Список студентов моей группы:
Держу пари, что никакой экстрасенс не сможет никогда догадаться о том, к какой из девочек своей группы я неравнодушен, и вообще, существует ли в моей группе такая девочка, к которой я не равнодушен. Потому что экстрасенсов не существует! Телепатия, предсказание, гадание и прочая туфта – всё это лженаука чистой воды. Нет в природе ничего паранормального и быть не может!
А вот интересный вопрос для размышления всем посетителям сайта:
Какое общество будет развиваться быстрее:
1. Общество, в котором люди соперничают и конкурируют
2. Общество, где все люди помогают друг другу и решают все задачи коллективным умом.
Я предполагаю, что второе общество будет более прогрессивным, и, на мой взгляд, взаимопомощь, а не борьба приводит к развитию. Но как это доказать?
На главную страницу