Координаты центра описанной вокруг тетраэдра сферы.
Радиус описанной вокруг тетраэдра сферы.
Пусть A(xa, ya, za), B(xb, yb, zb), C(xc, yc, zc), S(xs, ys, zs) – вершины тетраэдра,bgColor="#F0E68C" O(xo, yo, zo) – центр описанной вокруг тетраэдра SABC сферы радиуса R
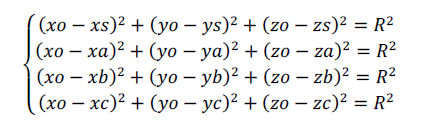
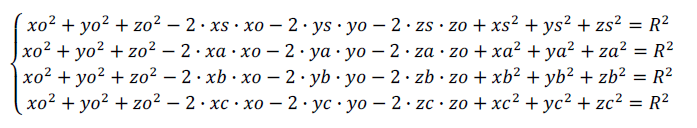
Из второго, третьего и четвёртого уравнения вычистаем первое:
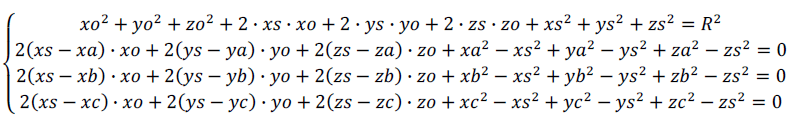

По формулам Крамера:

В знаменателе стоит отличное от нуля смешанное произведение векторов AS, BS, CS, равное по модулю утроенному объёму данного тетраэдра SABC. Поэтому у данной системы сущестует единственное решение.
Центр описанной вокруг тетраэдра сферы имеет координаты:

Радиус описанной сферы:
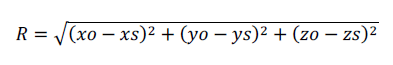
На главную страницу.