Задано n произвольных натуральных чисел.
Найти все суммы по k чисел, сумма которых равна заданному числу m.
Архив программы для wxDev-C++.
Код программы.
Проверка нахождения всх сочетаний из n элементов по k элементов.
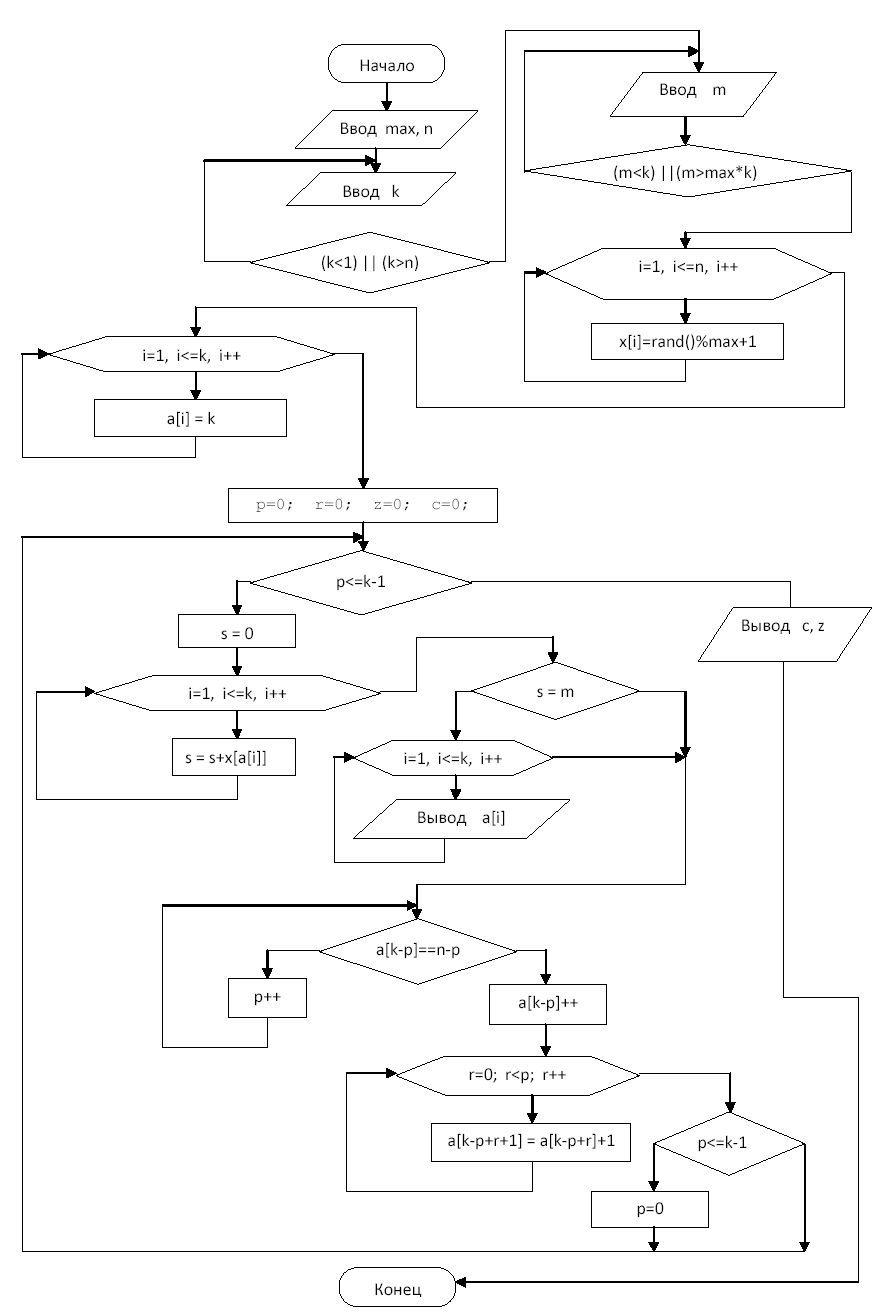
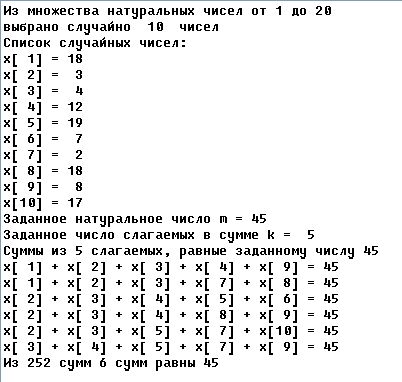
Данная программа создаст массив из n случайных натуральных чисел из множества 1..max, где числа max, n задаются с клавиатуры. После этого задаётся число слагаемых k и натуральное число m, которое не меньше числа слагаемых k и не больше произведения k*max. Программа вычисляет всевозможные суммы из k слагаемых, сравнивает эти суммы с заданным числом m и выводит на экран и в текстовый файл сomb.txt номера индексов тех элементов массива, сумма которых равна заданному числу m.
Вводится число n – количество элементов массива x[i].
Вводится максимальное натуральное число max, которое может присутствовать среди этих чисел.
Вводится число слагаемых в суммах k. При этом проверяется условие 1<=k<=n. В том случае, если это условие не выполняется, происходит повторный ввод этого числа.
Вводится заданное число m. При этом проверяется условие k<=m<=max*k. В том случае, если это условие не выполняется, происходит повторный ввод этого числа.
После этого вводится массив x[i] из n случайных натуральных чисел, не превосходящих числа max. Индекс i меняется при этом от 1 до n в цикле.
После этого вводится массив из k индексов a[i] для k слагаемых в сумме. В начальной конфигурации все эти индексы следуют по порядку друг за другом от 1 до k. Индекс i меняется при этом от 1 до k в цикле for (i=0; i ≤ k; i++) a[i]=i; .
Далее присваиваются нулевые значения элементам p, r, z, c.
c – это количество сочетаний из n элементов по k элементов, то есть общее количество сумм из k слагаемых.
z – количество сумм, равных заданному элементу m.
p – переменная, указывающая, сколько элементов индексов в конце массива индексов удовлетворяют условию: a[k-p]==n-p, то есть последний элемент a[k] в списке a[1]..a[k] равен последнему номеру n , предпоследний a[k-1] равен n-1, … , p-й индекс с конца a[k-p] равен n-p. Значение переменной p будет меняться от 0 до k-1.
Далее следует большой цикл, который будет завершён тогда, когда значение переменной p станет равным k-1. Этот цикл закончится тогда, когда все k индексов в сумме станут располагаться по порядку друг за другом, и на последнем месте будет стоять индекс a(n), на предпоследнем a(n-1), … , на первом месте a(n-k+1).
Вычисляется сумма k слагаемых x[a[1]]+x[a[2]]+…+x[a[k]], и если эта сумма равна заданному числу m, то значения индексов слагаемых суммы выводится на экран и в файл. Если число заданное количество элементов массива n больше заданного количества слагаемых в сумме k (k<n), то в самой первой сумме, когда слагаемые располагались по порядку друг за другом a[1]=1, a[2]=2, … a[k]=k, а p=0, условие a[k-p]==n-p не выполняется, и значение последнего индекса a[k] увеличивается на единицу (a[k-p]++), после чего снова подсчитывается сумма k слагаемых x[a[1]]+x[a[2]]+… +x[a[k]], и если эта сумма равна заданному числу m, то значения индексов слагаемых суммы выводится на экран и в файл.
(Цикл for (r=0; r<p; r++) a[k-p+r+1]=a[k-p+r]+1; не выполняется ни разу при условии p==0).
Так продолжается до тех пор, пока последний индекс a[k]не станет равным n.
Как только начнёт выполняться условие a[k]==n (то есть a[k-p]==n-p при p==0), значение p увеличивается на единицу и принимает значение 1.
Если заданное n значительно больше заданного k, то при p==1 условие a[k-p]==n-p не выполняется, и значение предпоследнего индекса a[k-1] увеличивается на единицу a[k-1]= a[k-1]+1 (a[k-p]++ при p==1), а значение последнего индекса устанавливается на единицу больше значения предпоследнего индекса a[k]=a[k-1]+1 (это будет достигнуто благодаря однократному выполнению цикла for (r=0; r<p; r++) a[k-p+r+1]=a[k-p+r]+1; при значениях p==1, r==0).
После этого значение p присваивается нулевое значение и повторяется цикл с увеличением на 1 последнего индекса a[k].
На определённом этапе выполнения этого алгоритма может оказаться так, что p индексов подряд, начиная с конца массива индексов, удовлетворяют следующему условию:
a[k]==n, a[k-1]==n-1, a[k-2]==n-2, a[k-3]==n-3, … , a[k-p+1]==n-p+1,
но значение a[k-p] не равно n-p. Тогда происходит увеличение на единицу этого индекса a[k-p], а следующие за ним p индексов будут расположены по порядку возрастания на 1 друг за другом, то есть
a[k-p+1]=a[k-p]+1, a[k-p+2]=a[k-p+1]+1, a[k-p+3]= a[k-p+2]+1, … , a[k-1]=a[k-2]+1; a[k]=a[k-1]+1. )
Это произойдёт благодаря выполнению p раз цикла for (r=0; r<p; r++) a[k-p+r+1]=a[k-p+r]+1).
Большой цикл завершится при выполнении условия
a(k)==n, a(k-1)==n-1, a(k-2)==n-2, …, a(1)==n-k+1 На экран и в файл будут выведены всевозможные суммы из по k чисел, сумма которых равна заданному числу m.
После этого на экран и в файл выводятся количество таких сумм z, равных числу m, и общее количество сумм c