Задача о ранце. Программивание на языке СИ.
Известен вес P[1], P[2], ,,,, P[n] каждого из n предметов.Как разместить их в наименьшем числе рюкзаков, если грузоподъёмность каждого рюкзака равна q.
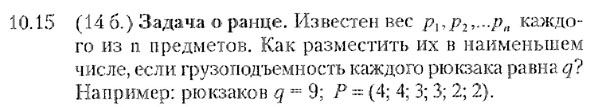
Просмотреть код программы.
Скачать архив программы.
Алгоритм работы программы.
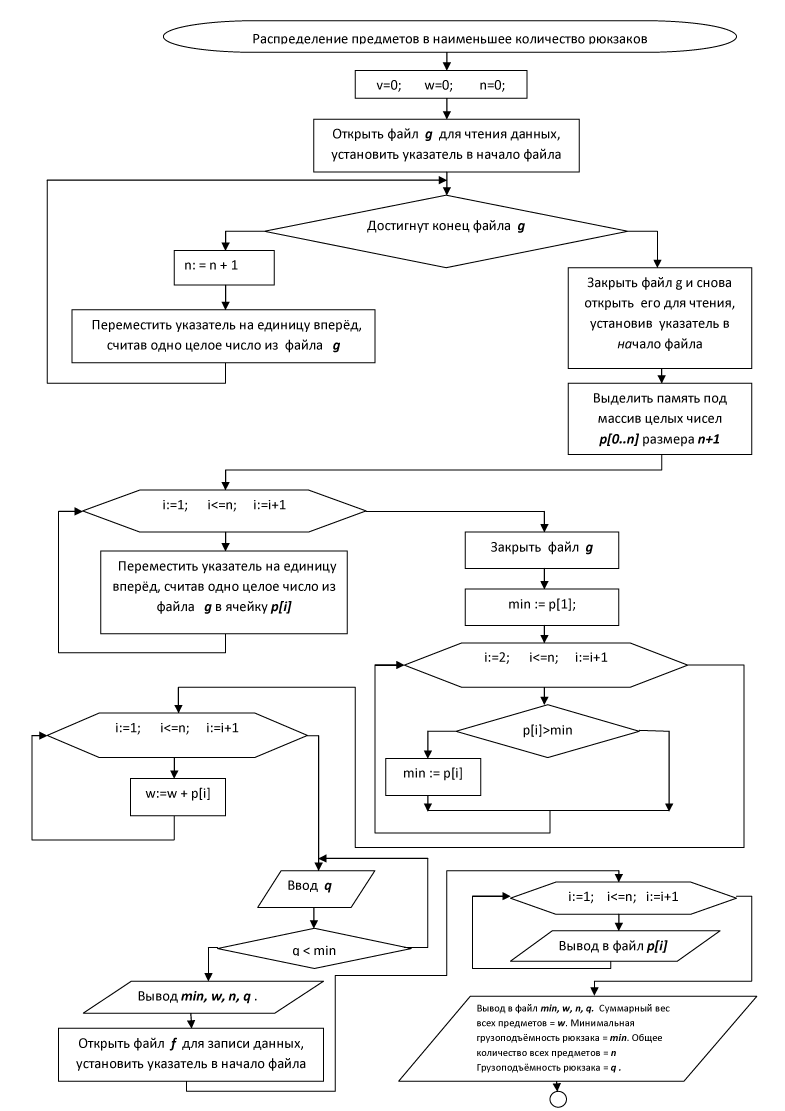
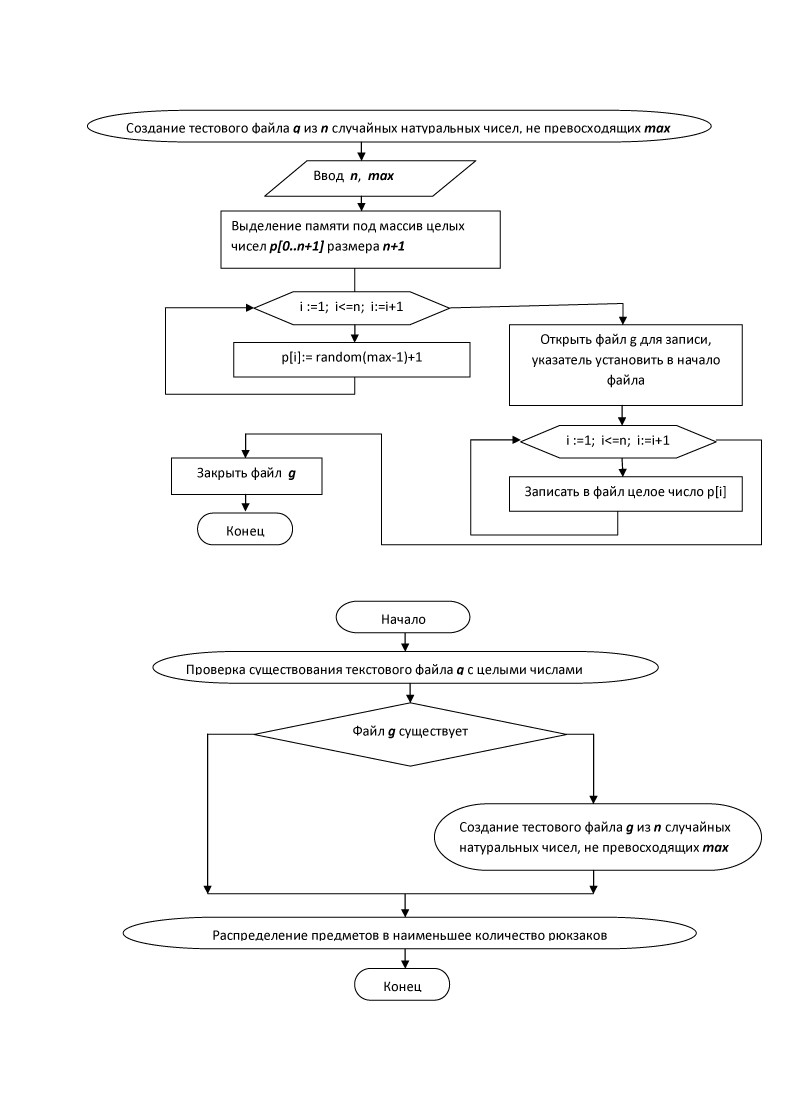
Программа проверяет, существует ли в папке с программой текстовый файл store.txt из действительных чисел, которые представляют собой вес каждого предмета, и если этого файла нет, то создаёт его. При создании файла требуется ввести количество всех предметов n и максимальную величину веса предмета, соответствующую минимальной грузоподъёмности рюкзака min. Если файл store.txt существует в папке с программой, выполняется подпрограмма, распределяющая предметы в наименьшее количество рюкзаков. Вначале количеству рюкзаков v, суммарному весу предметов w, количеству всех предметов n присваивается нулевое значение. Программа сначала подсчитывает количество всех предметов n (количество целых чисел, содержащихся в файле g). После этого выделяется память под массив целых чисел p[0..n], и все целые числа из файла store.txt записываются в массив p[n]. После этого находится максимальный элемента массива p[n], равный минимальной вместимости рюкзака min. Подсчитывается также суммарный вес всех предметов w, равный сумме всех элементов массива p(n). После этого пользователь сможет вести с клавиатуры значение минимальной вместимости рюкзака, не меньшее, чем min. Значения min, w, n, q, а также значения всех элементов массива p[n] выводятся на экран и в текстовый файл comb.txt
В начале работы программы в массиве p(n) все n чисел строго положительны, нулевых элементов нет. В процессе работы программы в порядке невозрастания числа m на экран и в файл comb.txt будут выводиться всевозможные суммы по k слагаемых, не содержащие в себе нулевых слагаемых и равные заданному числу m. Значение k количества слагаемых в этих суммах будет меняться от 1 до n. После вывода каждой такой суммы соответствующим слагаемым массива будет присваиваться нулевое значение, и следующие суммы будут состоять только из оставшихся ненулевых элементов массива. Сначала значению m будет присвоено значение вместимости рюкзака q , найдены и выведены все суммы, равные q, соответствующие рюказаку, заполненному максимально (вес всех предметов в рюкзаке равен вместимости рюкзака). После этого число m будем уменьшать на единицу и до суммы всех оставшихся ненулевых элементов массива, пока оно не станет равным нулю.
Для нахождения всевозможных сумм из из k слагаемых, равных заданному числу m, где каждое слагаемое суммы принадлежит множеству из n чисел p[1]..p[n], используется следующий алгоритм.
Вводится массив из k индексов a[i] для k слагаемых в сумме. В начальной конфигурации все эти индексы следуют по порядку друг за другом от 1 до k. Индекс i меняется при этом от 1 до k в цикле for (i=0; i<=k; i++) a[i]=i;.
Далее присваиваются нулевые значения элементам j, r.
j - переменная, указывающая, сколько элементов индексов в конце массива индексов удовлетворяют условию: a[k-j]==n-j, то есть последний элемент a[k] в списке a[1]..a[k] равен последнему номеру n , предпоследний a[k-1] равен n-1, …, j-й индекс с конца a[k-j] равен n-j. Значение переменной j будет меняться от 0 до k-1.
Далее следует большой цикл, который будет завершён тогда, когда значение переменной j станет равным k-1. Этот цикл закончится тогда, когда все k индексов в сумме станут располагаться по порядку друг за другом, и на последнем месте будет стоять индекс a(n), на предпоследнем a(n-1), …, на первом месте a(n-k+1).
Вычисляется сумма k слагаемых p[a[1]]+p[a[2]]+…+p[a[k]], и выполняется проверка, равна ли она заданному числу m. Если заданное количество элементов массива n больше заданного количества слагаемых в сумме k (k<n), то в самой первой сумме, когда слагаемые располагались по порядку друг за другом a[1]=1, a[2]=2, … a[k]=k, а j=0, условие a[k-j]==n-j не выполняется, и значение последнего индекса a[k] увеличивается на единицу (a[k-j]++), после чего снова подсчитывается сумма k слагаемых p[a[1]]+p[a[2]]+…+p[a[k]], и выполняется проверка, равна ли эта сумма равна заданному числу m.
(Цикл for (r=0; r<j; r++) a[k-j+r+1]=a[k-j+r]+1; не выполняется ни разу при условии j==0).
Так продолжается до тех пор, пока последний индекс a[k]не станет равным n.
Как только начнёт выполняться условие a[k]==n (то есть a[k-j]==n-j при j==0), значение j увеличивается на единицу и принимает значение 1.
Если заданное n значительно больше заданного k, то при j==1 условие a[k-j]==n-j не выполняется, и значение предпоследнего индекса a[k-1] увеличивается на единицу a[k-1]= a[k-1]+1 (a[k-j]++ при j==1), а значение последнего индекса устанавливается на единицу больше значения предпоследнего индекса a[k]=a[k-1]+1 (это будет достигнуто благодаря однократному выполнению цикла for (r=0; r<j; r++) a[k-j+r+1]=a[k-j+r]+1; при значениях j==1, r==0).
После этого значение j присваивается нулевое значение и повторяется цикл с увеличением на 1 последнего индекса a[k].
а определённом этапе выполнения этого алгоритма может оказаться так, что j индексов подряд, начиная с конца массива индексов, удовлетворяют следующему условию:
a[k]==n, a[k-1]==n-1, a[k-2]==n-2, a[k-3]==n-3, … , a[k-j+1]==n-j+1,
но значение a[k-j] не равно n-j. Тогда происходит увеличение на единицу этого индекса a[k-j], а следующие за ним j индексов будут расположены по порядку возрастания на 1 друг за другом, то есть
a[k-j+1]=a[k-j]+1, a[k-j+2]=a[k-j+1]+1, a[k-j+3]= a[k-j+2]+1, … , a[k-1]=a[k-2]+1; a[k]=a[k-1]+1. )
Это произойдёт благодаря выполнению j раз цикла for (r=0; r<j; r++) a[k-j+r+1]=a[k-j+r]+1).
Большой цикл завершится при выполнении условия
a(k)==n, a(k-1)==n-1, a(k-2)==n-2, …, a(1)==n-k+1 Так будут выведены всевозможные суммы из по k чисел, сумма которых равна заданному числу m.
Индекс k будет пробегать все значения от 1 до n

файл store.txt 4 4 3 3 2 2 Файл comb.txt ООбщее количество предметов N= 6 Вес каждого предмета: P[ 1] = 4 P[ 2] = 4 P[ 3] = 3 P[ 4] = 3 P[ 5] = 2 P[ 6] = 2 Грузоподъёмность рюкзака = 9 Суммарный вес всех предметов = 18 В 1 -й рюкзак вошли следующие предметы P[ 1] + P[ 3] + P[ 5] = 9 В 2 -й рюкзак вошли следующие предметы P[ 2] + P[ 4] + P[ 6] = 9 файл store.txt 22 16 24 4 8 15 11 13 15 4 15 19 27 28 14 22 4 10 20 3 Файл comb.txt Общее количество предметов N= 20 Вес каждого предмета: P[ 1] = 22 P[ 2] = 16 P[ 3] = 24 P[ 4] = 4 P[ 5] = 8 P[ 6] = 15 P[ 7] = 11 P[ 8] = 13 P[ 9] = 15 P[10] = 4 P[11] = 15 P[12] = 19 P[13] = 27 P[14] = 28 P[15] = 14 P[16] = 22 P[17] = 4 P[18] = 10 P[19] = 20 P[20] = 3 Грузоподъёмность рюкзака = 42 Суммарный вес всех предметов = 294 В 1 -й рюкзак вошли следующие предметы P[ 1] + P[19] = 42 В 2 -й рюкзак вошли следующие предметы P[ 6] + P[13] = 42 В 3 -й рюкзак вошли следующие предметы P[14] + P[15] = 42 В 4 -й рюкзак вошли следующие предметы P[ 2] + P[ 4] + P[16] = 42 В 5 -й рюкзак вошли следующие предметы P[ 3] + P[ 5] + P[18] = 42 В 6 -й рюкзак вошли следующие предметы P[ 7] + P[ 8] + P[ 9] + P[20] = 42 В 7 -й рюкзак вошли следующие предметы P[10] + P[11] + P[12] + P[17] = 42 Файл comb.txt Общее количество предметов N= 20 Вес каждого предмета: P[ 1] = 22 P[ 2] = 16 P[ 3] = 24 P[ 4] = 4 P[ 5] = 8 P[ 6] = 15 P[ 7] = 11 P[ 8] = 13 P[ 9] = 15 P[10] = 4 P[11] = 15 P[12] = 19 P[13] = 27 P[14] = 28 P[15] = 14 P[16] = 22 P[17] = 4 P[18] = 10 P[19] = 20 P[20] = 3 Грузоподъёмность рюкзака = 40 Суммарный вес всех предметов = 294 В 1 -й рюкзак вошли следующие предметы P[ 2] + P[ 3] = 40 В 2 -й рюкзак вошли следующие предметы P[ 8] + P[13] = 40 В 3 -й рюкзак вошли следующие предметы P[ 1] + P[ 4] + P[15] = 40 В 4 -й рюкзак вошли следующие предметы P[ 5] + P[10] + P[14] = 40 В 5 -й рюкзак вошли следующие предметы P[ 6] + P[ 9] + P[18] = 40 В 6 -й рюкзак вошли следующие предметы P[11] + P[16] + P[20] = 40 В 7 -й рюкзак вошли следующие предметы P[12] + P[19] = 39 В 8 -й рюкзак вошли следующие предметы P[ 7] + P[17] = 15