Нахождение минимума функции методом парабол.
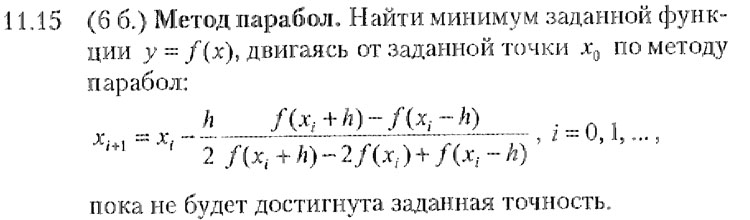
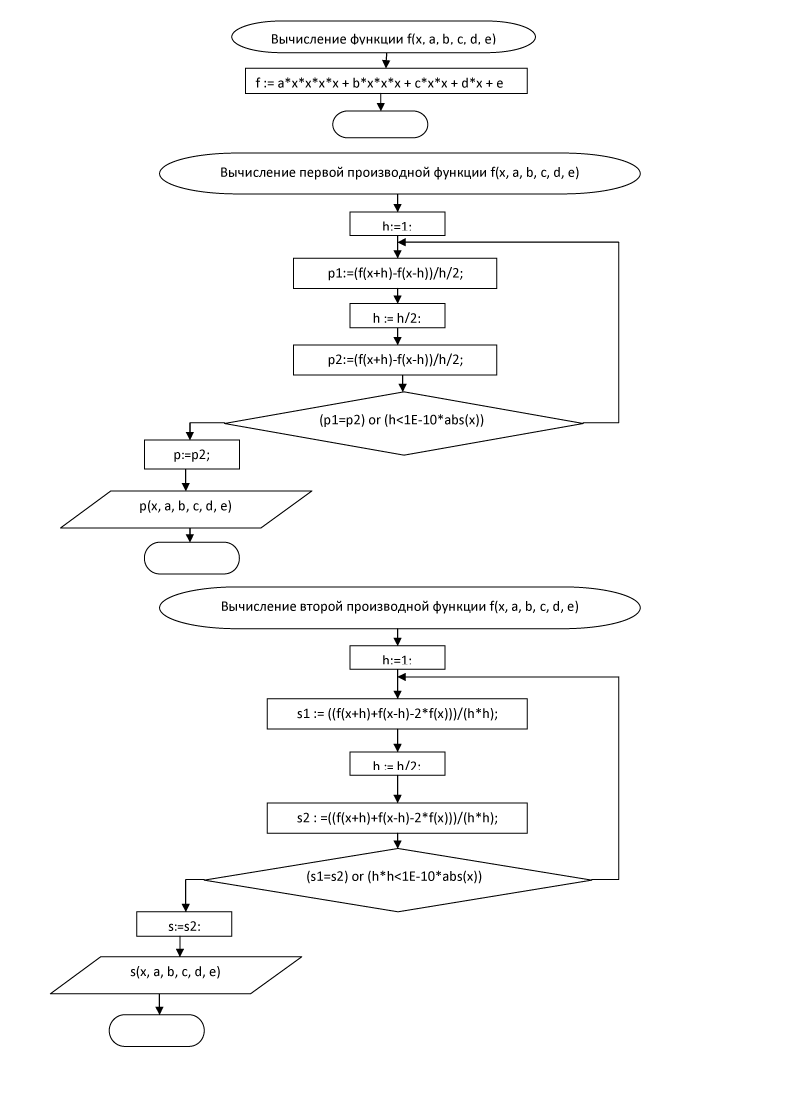
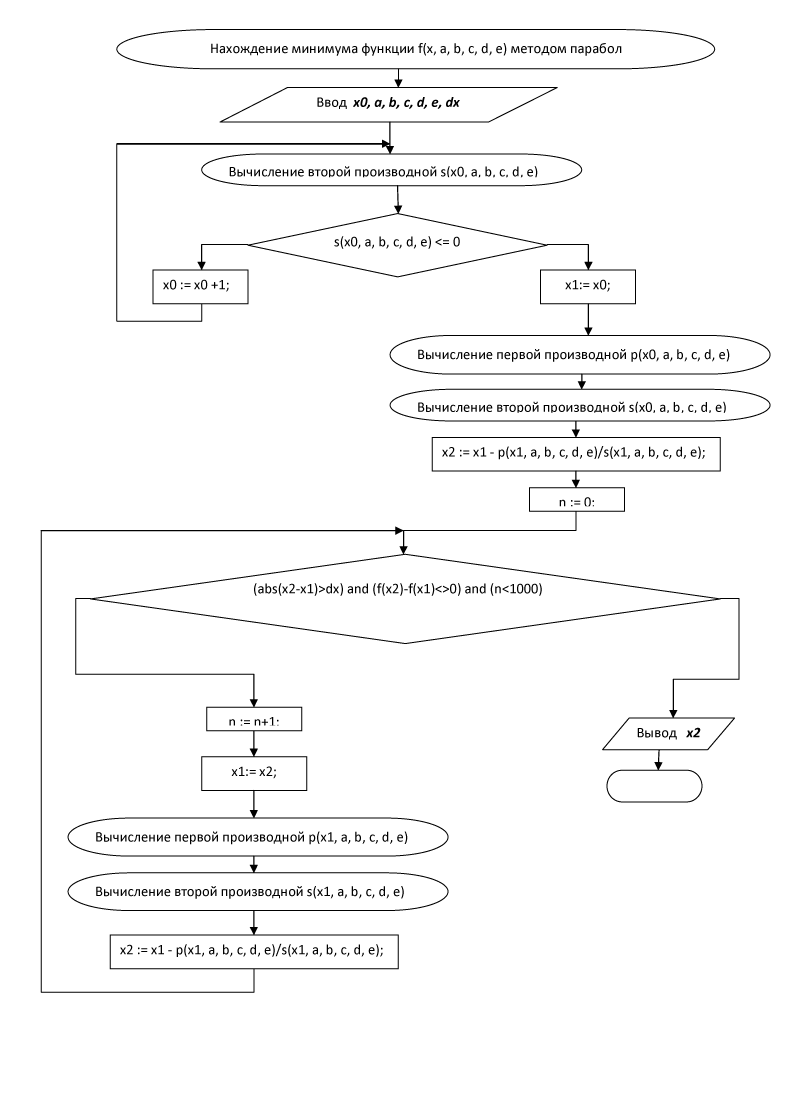
Алгоритм программы.
Код программы.
Скачать программу в архиве.
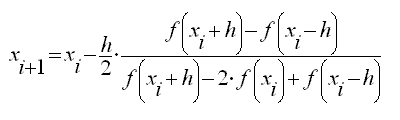
может обращаться в нуль, в результате чего произойдёт ошибка с кодом «деление на нуль».
Для предотвращения этой ошибки надо начать вычисления с точки, в которой вторая производная положительна, и итерационный процесс производить по равносильной формуле
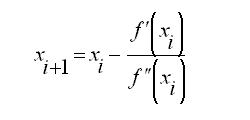
По формуле Тейлора приближаем функцию параболой
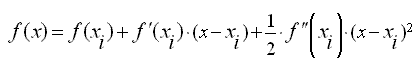
Если
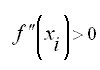
то эта парабола имеет вогнутость вниз и достигает своего минимума в точке
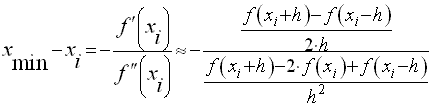
что доказывает равносильность формул
Напишем функцию вычисления первой производной, функцию вычисления второй производной, которые будем использовать при нахождении минимума функции.
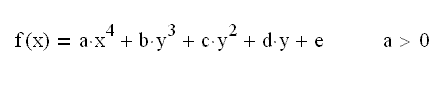
При вычислении первой производной в точке x будем уменьшать значение h в формуле

до тех пор, пока либо значение этого выражения при h и h/2 не станут равными друг другу, либо отношение h/x не станет меньше 0.0000000001, так как при h< 0.0000000001*x будут резко возрастать погрешности машинной арифметики. (1+0.0000000000000001=1)
При вычислении второй производной в точке x будем уменьшать значение h в формуле
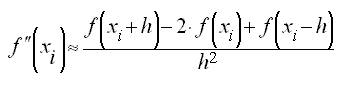
до тех пор, пока либо значение этого выражения при h и h/2 не станут равными друг другу, либо отношение h*h/x не станет меньше 0.0000000001.
При вычислении минимума функции
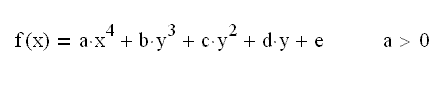
сначала вычислим значение второй производной в заданной точке x. Если условие
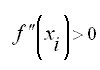
не выполнено, то график функции не имеет в заданной точки выпуклости вниз, то есть не может быть приближен параболой, ветви которой направлены вверх. Поэтому мы будем двигаться вправо с шагом 1 до тех пор, пока вторая производная не станет положительной, и выпуклость вниз не будет достигнута. После этого начинается рекурсивный алгоритм нахождения функции по формуле
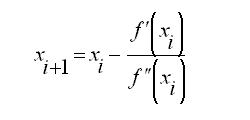
Алгоритм завершит работу, либо когда разность между соседними точками x[k+1] и x[k] станет меньше по абсолютной величине заданной погрешности dx, либо когда значения функции в точках [k+1] и x[k] станут равны друг другу.
На время тестирования программы для выявления исключительных случаев длительной работы программы целесообразно также ограничить цикл 1000 шагами.
Программа также выводит значение x[k], значения первой и второй производной в каждой точке x[k], приращение функции f(x[k+1])-f(x[k]).
В конце работы алгоритма выводится значение минимума функции.
Шесть чисел x, a, b, c, d, e являются формальными параметрами как самой функции, так и функций вычисления первой и второй производной функции.
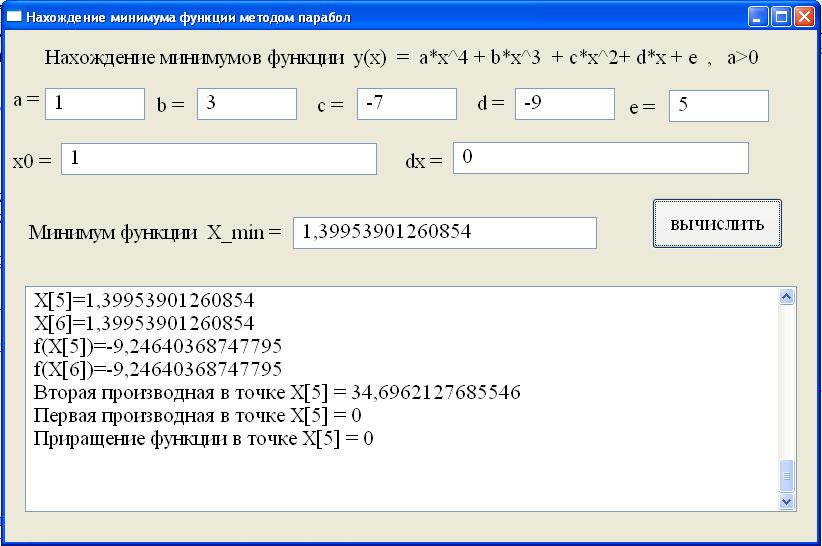
X[0]=1 X[0]=1 X[1]=1,625 f(X[0])=-7 f(X[1])=-8,263427734375 Вторая производная в точке X[0] = 16 Первая производная в точке X[0] = -10 Приращение функции в точке X[0] = -1,263427734375 X[1]=1,625 X[2]=1,4294274300932 f(X[1])=-8,263427734375 f(X[2])=-9,23067595172717 Вторая производная в точке X[1] = 46,9375 Первая производная в точке X[1] = 9,1796875 Приращение функции в точке X[1] = -0,96724821735217 X[2]=1,4294274300932 X[3]=1,40018058532794 f(X[2])=-9,23067595172717 f(X[3])=-9,24639654445609 Вторая производная в точке X[2] = 36,2488479614257 Первая производная в точке X[2] = 1,06016442924737 Приращение функции в точке X[2] = -0,01572059272891 X[3]=1,40018058532794 X[4]=1,39953931490417 f(X[3])=-9,24639654445609 f(X[4])=-9,24640368747637 Вторая производная в точке X[3] = 34,7293701171875 Первая производная в точке X[3] = 0,02227091789245 Приращение функции в точке X[3] = -7,14302028193004E-6 X[4]=1,39953931490417 X[5]=1,39953901260854 f(X[4])=-9,24640368747637 f(X[5])=-9,24640368747795 Вторая производная в точке X[4] = 34,6963500976562 Первая производная в точке X[4] = 0,00001048855483 Приращение функции в точке X[4] = -1,58273394390562E-12 X[5]=1,39953901260854 X[6]=1,39953901260854 f(X[5])=-9,24640368747795 f(X[6])=-9,24640368747795 Вторая производная в точке X[5] = 34,6962127685546 Первая производная в точке X[5] = 0 Приращение функции в точке X[5] = 0
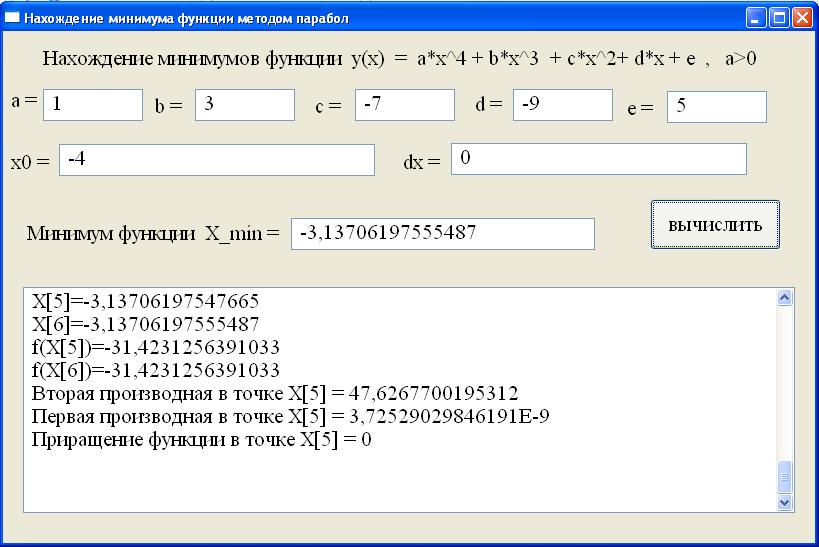
X[0]=-4 X[0]=-4 X[1]=-3,38679245283018 f(X[0])=-7 f(X[1])=-29,7853974063811 Вторая производная в точке X[0] = 106 Первая производная в точке X[0] = -65 Приращение функции в точке X[0] = -22,7853974063811 X[1]=-3,38679245283018 X[2]=-3,16754918597949 f(X[1])=-29,7853974063811 f(X[2])=-31,4007203761561 Вторая производная в точке X[1] = 62,6819458007812 Первая производная в точке X[1] = -13,7425945699214 Приращение функции в точке X[1] = -1,61532296977502 X[2]=-3,16754918597949 X[3]=-3,1376056494904 f(X[2])=-31,4007203761561 f(X[3])=-31,4231185987762 Вторая производная в точке X[2] = 49,3844604492187 Первая производная в точке X[2] = -1,47874539345502 Приращение функции в точке X[2] = -0,02239822262007 X[3]=-3,1376056494904 X[4]=-3,13706215271951 f(X[3])=-31,4231185987762 f(X[4])=-31,4231256391025 Вторая производная в точке X[3] = 47,6578979492187 Первая производная в точке X[3] = -0,02590191364288 Приращение функции в точке X[3] = -7,04032633791485E-6 X[4]=-3,13706215271951 X[5]=-3,13706197547665 f(X[4])=-31,4231256391025 f(X[5])=-31,4231256391033 Вторая производная в точке X[4] = 47,6267852783203 Первая производная в точке X[4] = -8,4415078163147E-6 Приращение функции в точке X[4] = -7,67386154620908E-13 X[5]=-3,13706197547665 X[6]=-3,13706197555487 f(X[5])=-31,4231256391033 f(X[6])=-31,4231256391033 Вторая производная в точке X[5] = 47,6267700195312 Первая производная в точке X[5] = 3,72529029846191E-9 Приращение функции в точке X[5] = 0
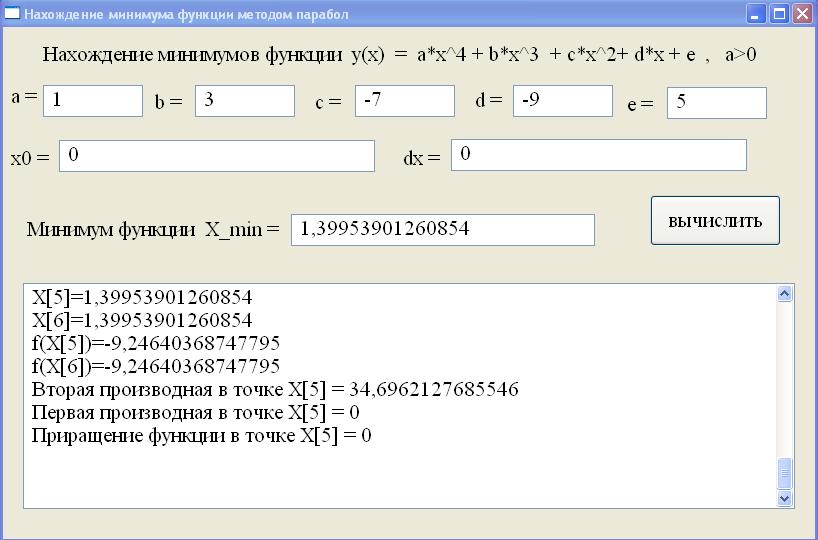
X[0]=0 Введённое начальное значение X[0] не соответствует вогнутости вниз Вторая производная в точке X[0] не является положительной = -14 X[0]=1 X[1]=1,625 f(X[0])=-7 f(X[1])=-8,263427734375 Вторая производная в точке X[0] = 16 Первая производная в точке X[0] = -10 Приращение функции в точке X[0] = -1,263427734375 X[1]=1,625 X[2]=1,4294274300932 f(X[1])=-8,263427734375 f(X[2])=-9,23067595172717 Вторая производная в точке X[1] = 46,9375 Первая производная в точке X[1] = 9,1796875 Приращение функции в точке X[1] = -0,96724821735217 X[2]=1,4294274300932 X[3]=1,40018058532794 f(X[2])=-9,23067595172717 f(X[3])=-9,24639654445609 Вторая производная в точке X[2] = 36,2488479614257 Первая производная в точке X[2] = 1,06016442924737 Приращение функции в точке X[2] = -0,01572059272891 X[3]=1,40018058532794 X[4]=1,39953931490417 f(X[3])=-9,24639654445609 f(X[4])=-9,24640368747637 Вторая производная в точке X[3] = 34,7293701171875 Первая производная в точке X[3] = 0,02227091789245 Приращение функции в точке X[3] = -7,14302028193004E-6 X[4]=1,39953931490417 X[5]=1,39953901260854 f(X[4])=-9,24640368747637 f(X[5])=-9,24640368747795 Вторая производная в точке X[4] = 34,6963500976562 Первая производная в точке X[4] = 0,00001048855483 Приращение функции в точке X[4] = -1,58273394390562E-12 X[5]=1,39953901260854 X[6]=1,39953901260854 f(X[5])=-9,24640368747795 f(X[6])=-9,24640368747795 Вторая производная в точке X[5] = 34,6962127685546 Первая производная в точке X[5] = 0 Приращение функции в точке X[5] = 0

На главную страницу.