Лабораторная работа №2 по предмету «Графическая визуализация».
Кривые Безье третьего порядка
Две вспомогательные точки при построении кривой Безье третьего порядка характеризуют не только направление касательной к кривой в конечных точках, но также вогнутость кривой в направлении касательных векторов. Первую кривую строим из опорной точки с координатами (100,200) длиной 400 в горизонтальном направлении, касательные векторы направлены вертикально в противоположных направлениях и имеют длину 200; левый вектор направлен вверх, правый - вниз:<path d="M 100,200 c 0,-200 400,200 400,0" style="fill: red"/ >
Вторая кривая, симметричная ей относительно горизонтальной оси, строится просто: направления векторов меняются на противоположные:
<path d="M 100,200 c 0,200 400,-200 400,0" style="fill: blue"/ >
Для построения повёрнутых кривых из других опорных точек приходится использовать несколько громоздкие вычисления. Зададимся целью повернуть эти две построенные кривые относительно точки с координатами (300, 200), то есть изобразить «пропеллер».
При повороте на угол Pi/3 против часовой стрелки, координаты опорной точки:
mx =300-200*cos(Pi/3)=200
my =200+200*sin(Pi/3)=373.2
Относительные координаты конечной точки относительно опорной:
x =400*сos(Pi/3)=200
y =-400*sin(Pi/3)= -346.4
Относительные координаты первой дополнительной точки относительно опорной точки находятся как координаты вектора (0, -200), повернутого на Pi/3 против часовой стрелки:
x1 = -200*sin(Pi/3)=-173.2
y1 = -200*cos(Pi/3)=-100
Относительные координаты второй дополнительной точки относительно опорной точки находятся, как координаты конца вектора (0, 200), повернутого на Pi/3 против часовой стрелки, начало которого приложено в конечной точке кривой :
x2 = 400*сos(Pi/3)+200*sin(Pi/3)=373.2
y2 = -400*sin(Pi/3)+200*cos(Pi/3)=-246.4
<path d="M 200,373.2 c -173.2,-100 373.2,-246.4 200,-346.4" style="fill: red"/ >
Для второй кривой координаты первой дополнительной точки:
x1 = 200*sin(Pi/3)=173.2
y1 = 200*cos(Pi/3)=100
Координаты второй дополнительной точки
x2 = 400*сos(Pi/3)-200*sin(Pi/3)=26.8
y2= -400*sin(Pi/3)-200*cos(Pi/3)=-446.4
<path d="M 200,373.2 c 173.2,100 26.8,-446.4 200,-346.4" style="fill: blue"/ >
При повороте на угол Pi/3 по часовой стрелке координаты опорной точки:
mx = 300-200*cos(Pi/3)=200
my = 200-200*sin(Pi/3)=26.8
Относительные координаты конечной точки относительно опорной:
x = 400*сos(Pi/3)=200
y = 400*sin(Pi/3)= 346.4
Относительные координаты первой дополнительной точки относительно опорной точки находятся как координаты вектора (0, -200), повернутого на Pi/3 по часовой стрелке:
x1 = 200*sin(Pi/3)=173.2
y1 = -200*cos(Pi/3)=-100
Относительные координаты второй дополнительной точки относительно опорной точки находятся, как координаты конца вектора (0, 200), повернутого на Pi/3 по часовой стрелке, начало которого приложено в конечной точке кривой :
x2 = 400*сos(Pi/3)-200*sin(Pi/3)=26.8
y2 = 400*sin(Pi/3)+200*cos(Pi/3)=446.4
<path d="M 200,26.8 c 173.2,-100 26.8,446.4 200,346.4" style="fill: red"/ >
Для второй кривой координаты первой дополнительной точки:
x1 = -200*sin(Pi/3)=-173.2
y1 = 200*cos(Pi/3)=100
Координаты второй дополнительной точки
x2 = 400*сos(Pi/3)+200*sin(Pi/3)=373.2
y2 = 400*sin(Pi/3)-200*cos(Pi/3)=246.4 <path d="M 200,26.8 c -173.2,100 373.2, 246.4 200,346.4" style="fill: blue"/ >
Код рисунка №1.
<?xml version="1.0" encoding="utf-8"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg width="600" height="400"> <circle cx="300" cy="200" r="200" fill="yellow"/> <path d="M 100, 200 c 0, 200 400, -200 400, 0" style="fill: blue"/> <path d="M 100, 200 c 0, -200 400, 200 400, 0" style="fill: red"/> <path d="M 200, 373.2 c -173.2, -100 373.2, -246.4 200, -346.4" style="fill: red"/> <path d="M 200, 373.2 c 173.2, 100 26.8, -446.4 200, -346.4" style="fill: blue"/> <path d="M 200, 26.8 c 173.2, -100 26.8, 446.4 200, 346.4" style="fill: red"/> <path d="M 200, 26.8 c -173.2, 100 373.2, 246.4 200, 346.4" style="fill: blue"/> </svg>
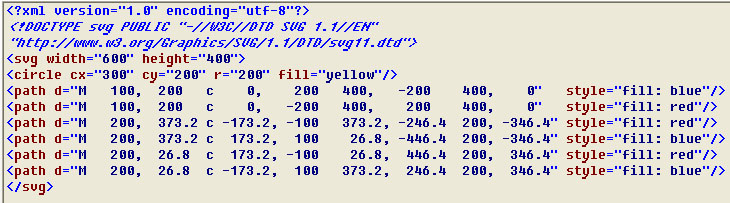
SVG lab02p1.svg
Кривые Безье четвертого порядка
Попробуем тот же рисунок построить при помощи квадратичных кривых.Четыре кривые имеют код:
<path d="M 100,200 q 0, 120 200,0" style="fill: blue"/ >
<path d="M 100,200 q 0,-120 200,0" style="fill: red"/ >
<path d="M 500,200 q 0,-120 -200,0" style="fill: blue"/ >
<path d="M 500,200 q 0, 120 -200,0" style="fill: red"/ >
Модуль проекции вектора (0,120), повёрнутого на угол Pi/3:
на горизонтальную ось : 120*sin(Pi/3)=103.9,
а на вертикальную ось 120*cos(Pi/3)=60,
Модуль проекции вектора (200, 0), повёрнутого на угол Pi/3,
на горизонтальную ось: 200*cos(Pi/3)=100,
на вертикальную ось: 200*sin(Pi/3)=173.2
<path d="M 200, 373.2 q 103.9 60 100, -173.2" style="fill: blue"/ >
<path d="M 200, 373.2 q -103.9, -60 100, -173.2" style="fill: red"/ >
<path d="M 400, 26.8 q -103.9 -60 -100, 173.2" style="fill: blue"/ >
<path d="M 400, 26.8 q 103.9, 60 -100, 173.2" style="fill: red"/ >
<path d="M 200, 26.8 q -103.9 60 100, 173.2" style="fill: blue"/ >
<path d="M 200, 26.8 q 103.9, -60 100, 173.2" style="fill: red"/ >
<path d="M 400, 373.2 q 103.9 -60 -100, -173.2" style="fill: blue"/ >
<path d="M 400, 373.2 q -103.9, 60 -100, -173.2" style="fill: red"/ >
Код рисунка №2:
<?xml version="1.0" encoding="utf-8"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg width="600" height="400"> <circle cx="300" cy="200" r="200" fill="yellow"/> <path d="M 100, 200 q 0, 120 200, 0" style="fill: blue"/> <path d="M 100, 200 q 0, -120 200, 0" style="fill: red"/> <path d="M 500, 200 q 0, -120 -200, 0" style="fill: blue"/> <path d="M 500, 200 q 0, 120 -200, 0" style="fill: red"/> <path d="M 200, 373.2 q 103.9, 60 100, -173.2" style="fill: blue"/> <path d="M 200, 373.2 q -103.9, -60 100, -173.2" style="fill: red"/> <path d="M 400, 26.8 q -103.9, -60 -100, 173.2" style="fill: blue"/> <path d="M 400, 26.8 q 103.9, 60 -100, 173.2" style="fill: red"/> <path d="M 200, 26.8 q -103.9, 60 100, 173.2" style="fill: blue"/> <path d="M 200, 26.8 q 103.9, -60 100, 173.2" style="fill: red"/> <path d="M 400, 373.2 q 103.9, -60 -100, -173.2" style="fill: blue"/> <path d="M 400, 373.2 q -103.9, 60 -100, -173.2" style="fill: red"/> </svg>
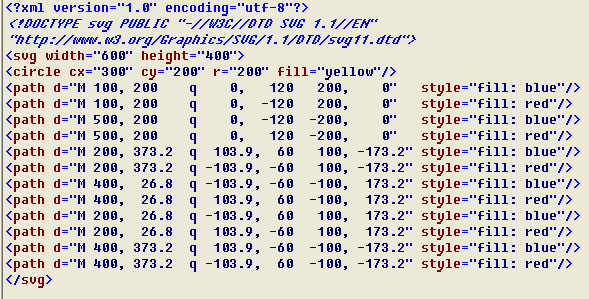
Рисунок SVG lab02p2.svg
Сравнение кривых Безье третьего и четвёртого порядка.
Код рисунка №3<?xml version="1.0" encoding="utf-8"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg width="600" height="400"> <circle cx="300" cy="200" r="200" fill="none; stroke:green"/> <path d="M 100, 200 c 0, 200 400, -200 400, 0" style="fill: none; stroke:red"/> <path d="M 100, 200 c 0, -200 400, 200 400, 0" style="fill: none; stroke:red"/> <path d="M 200, 373.2 c -173.2, -100 373.2, -246.4 200, -346.4" style="fill: none; stroke:red"/> <path d="M 200, 373.2 c 173.2, 100 26.8, -446.4 200, -346.4" style="fill: none; stroke:red"/> <path d="M 200, 26.8 c 173.2, -100 26.8, 446.4 200, 346.4" style="fill: none; stroke:red"/> <path d="M 200, 26.8 c -173.2, 100 373.2, 246.4 200, 346.4" style="fill: none; stroke:red"/> <path d="M 100, 200 q 0, 120 200, 0" style="fill: none; stroke:blue"/> <path d="M 100, 200 q 0, -120 200, 0" style="fill: none; stroke:blue"/> <path d="M 500, 200 q 0, -120 -200, 0" style="fill: none; stroke:blue"/> <path d="M 500, 200 q 0, 120 -200, 0" style="fill: none; stroke:blue"/> <path d="M 200, 373.2 q 103.9, 60 100, -173.2" style="fill: none; stroke:blue"/> <path d="M 200, 373.2 q -103.9, -60 100, -173.2" style="fill: none; stroke:blue"/> <path d="M 400, 26.8 q -103.9, -60 -100, 173.2" style="fill: none; stroke:blue"/> <path d="M 400, 26.8 q 103.9, 60 -100, 173.2" style="fill: none; stroke:blue"/> <path d="M 200, 26.8 q -103.9, 60 100, 173.2" style="fill: none; stroke:blue"/> <path d="M 200, 26.8 q 103.9, -60 100, 173.2" style="fill: none; stroke:blue"/> <path d="M 400, 373.2 q 103.9, -60 -100, -173.2" style="fill: none; stroke:blue"/> <path d="M 400, 373.2 q -103.9, 60 -100, -173.2" style="fill: none; stroke:blue"/> </svg>

Рисунок SVG lab02p3.svg
Выводы. Преобразование поворота кривой Безье третьего порядка потребовало весьма много вычислений. Аналогичное преобразование кривой Безье четвёртого порядка было менее трудоёмко. Выяснен только смысл двух дополнительных точек для кривой Безье третьего порядка как направлений касательных векторов в её крайних точках, но остался неисследованным параметр длины каждого такого касательного вектора. Поэтому остаётся неясным, график какой конкретной функции представляет из себя данная кубическая кривая Безье. Таким образом, использование кубической кривой Безье представляет интерес пока только для художника, но не для математика.
Изучение кривой Безье четвёртого порядка.
<?xml version="1.0" encoding="utf-8"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg width="600" height="400"> <path d="M 100,50 q 200, 200 400, 0" style="fill: none; stroke: blue; stroke-width:2 "/> <path d="M 100,50 l 200, 200 200, -200 z" style="fill: none; stroke: red"/> <path d="M300, 50 l 0, 100 z"/> </svg>
Рисунок SVG lab02p4.svg
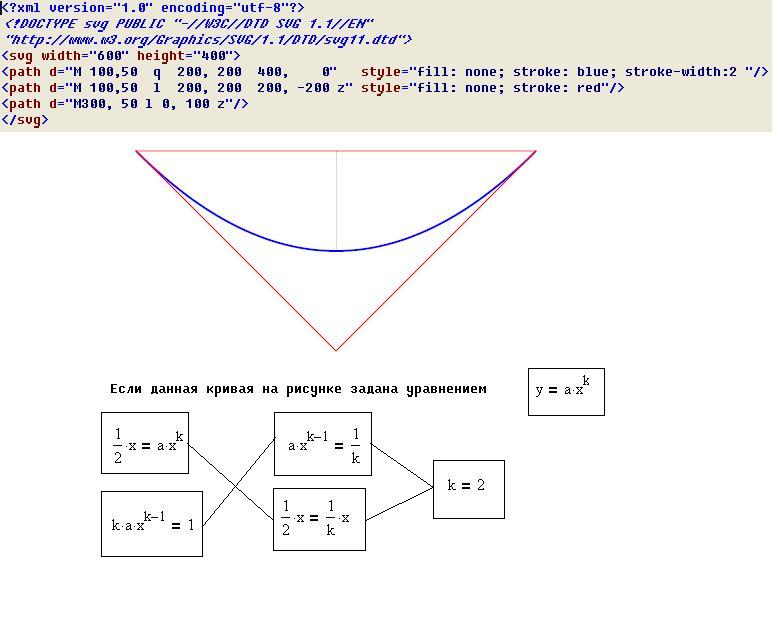
Отсюда можно сделать вывод, что данная кривая является кривой не четвёртого порядка, а кривой второго порядка, то есть обыкновенной параболой y=a*x^2. Если за единицу измерения выбрать 100 пикселей, то можно найти коэффициент a=1/4. Уравнение данной кривой y=1/4*x^2
<?xml version="1.0" encoding="utf-8"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg width="600" height="400"> <path d="M 100, 50 q 200, 350 400, 0" style="fill: none; stroke: blue; stroke-width:2"/> <path d="M 100, 50 l 200, 350 200, -350 z" style="fill: none; stroke: red"/> <path d="M300, 50 l 0, 175 z"/> </svg>
Рисунок SVG lab02p5.svg
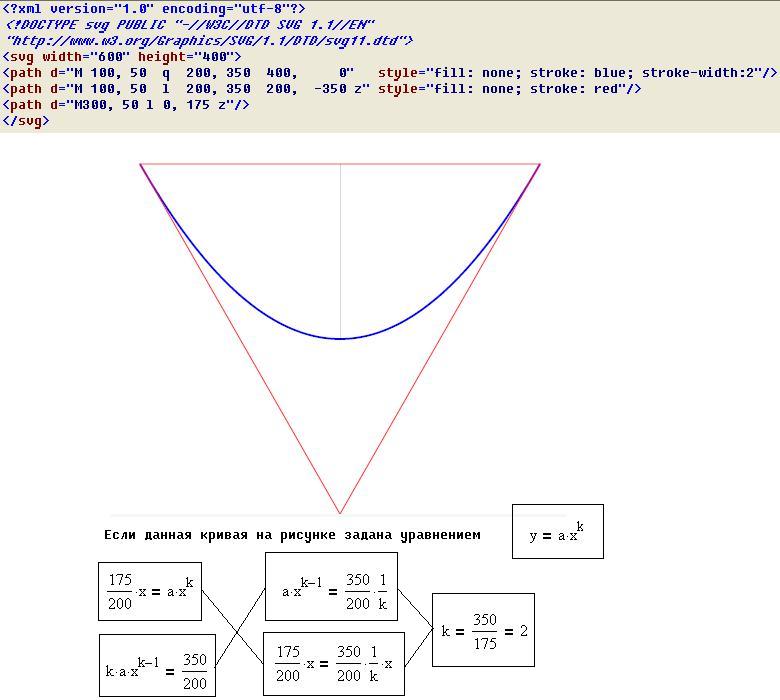
И в этом случае снова получилась парабола, кривая, заданная уравнением второй степени. Если за единицу измерения выбрать 100 пикселей, то можно найти коэффициент a=7/16. Уравнение данной кривой y=7/16*x^2
Вывод. Кривая Безье четвёртого порядка представляет собой параболу y=a*x^2, при условии, когда абсцисса дополнительной точки явлется полусуммой абсцисс крайних точек.
На главную страницу.