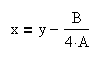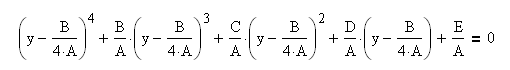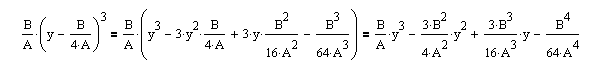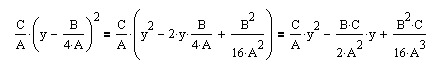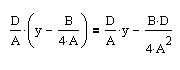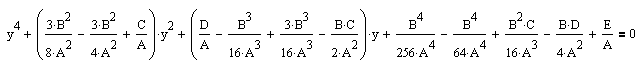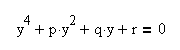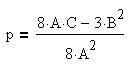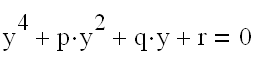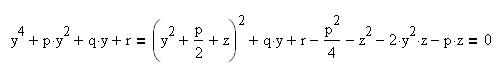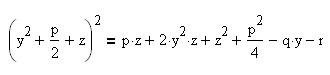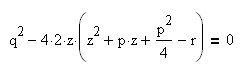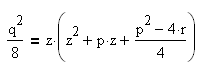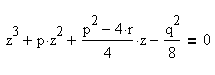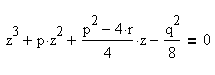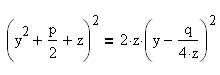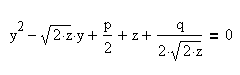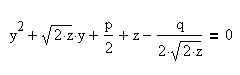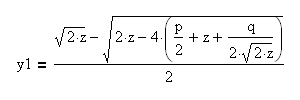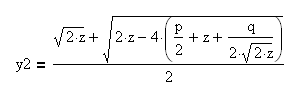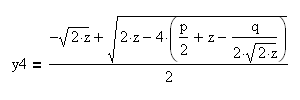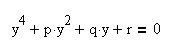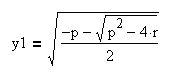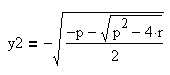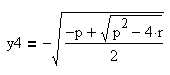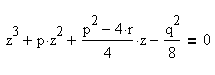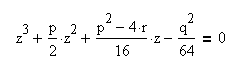Алгебраическое уравнение четвёртой степени.

1. Приведение уравнения к каноническому виду.
Сделаем замену переменного по формуле:
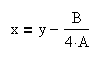
Получим уравнение:
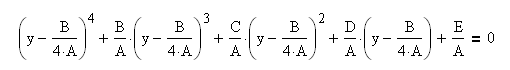
Раскроем скобки:

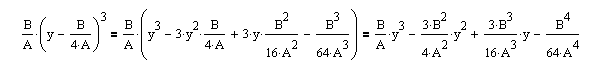
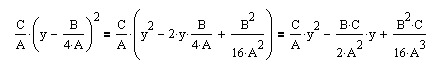
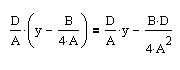
Получим уравнение:
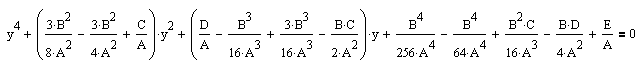


Уравнение приведено к каноническому виду:
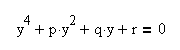
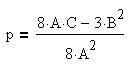


2. Решение уравнения
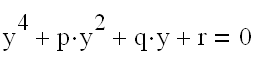
Способ №1.
Решение при помощи разложения на два квадратных уравнения
Рассмотрим случай, когда q не равно нулю.
Верно тождество:

Поэтому:
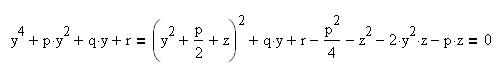
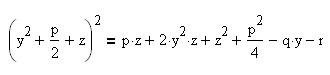
Получили уравнение:

Выберем параметр z так, чтобы правая часть этого уравнения была полным квадратом относительно y. Для этого необходимо и достаточно, чтобы дискриминант из коэффициентов трехчлена относительно y, стоящего справа, обращался в нуль:
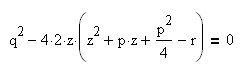
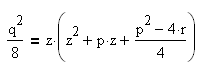
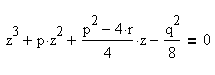
Мы получили кубическое уравнение.
Вывод формул кубичекого уравнения.
Если z - один из корней кубического уравнения:
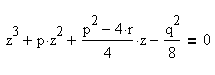
то уравнение

запишется в виде:
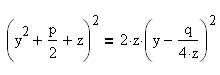
Отсюда следует:

Необходимо решить два квадратных уравнения:
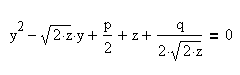
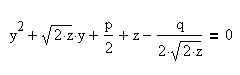
Получаем четыре корня:
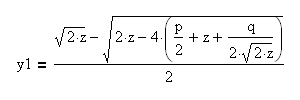
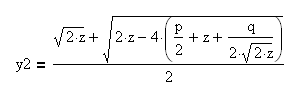

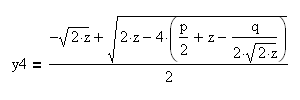
Корни этих квадратных уравнений y1, y2, y3, y4 являются решением исходного уравнения
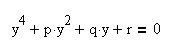
Рассмотрим случай, когда q=0
Уравнение

имеет четыре корня:
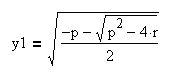
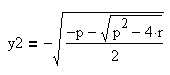

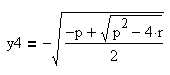
Способ №2.
Решение Декарта-Эйлера.
Обоснование этого способа решения уравнения четвёртой степени находится в стадии разработки.
 Эта программа находит четыре корня уравнения четвёртой степени двумя способами
Эта программа находит четыре корня уравнения четвёртой степени двумя способами
Способ №1.
Решение при помощи разложения на два квадратных уравнения
Если q не равно нулю, то кубическое уравнение
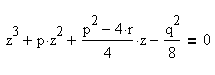
всегда имеет положительный действительный корень, так как при z=0 значение многочлена в левой части уравнения отрицательно: -q^2/8, а при стремлении z к плюс бесконечности значение многочлена в левой части уравнения также стремится к плюс бесконечности, то есть становится положительным при некотором положительном z=M, и так как непрерывная на отрезке [0; M] функция принимает на интервале (0; M) любое промежуточное, в том числе и нулевое, значение, то существует положительный корень этого кубического уравнения. Таким положительным корнем является либо первый корень в программе решения кубического уравнения, где под знаком косинуса стоит аргумент F/3, так как Cos(F/3)≥0 при 0≤F≤3/2*Pi, если кубическое уравнение имеет три различных действительных корня, либо единственный действительный корень этого кубического уравнения.
Если какой-то из действительных корней кубического уравнения принимает нулевое значение, то решается биквадратное уравнение

Способ №2.
Решение Декарта-Эйлера.
После приведения алгебраического уравнения четвёртой степени к каноническому виду программа находит три корня кубического уравнения
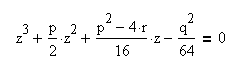
Если это кубическое уравнение имеет три действительных положительных корня, то уравнение четвёртой степени имеет четыре действительных корня.
Если это кубическое уравнение имеет три действительных корня, один положительный и два отрицательных, то уравнение четвёртой степени имеет две пары комплексно-сопряжённых корней.
Если это кубическое уравнение имеет один положительный действительный корень и два комплексно сопряжённые корня, то уравнение четвёртой степени имеет два действительных и два комплексно-сопряжённых корня.
Программа на javascript «Решение уравнения четвёртой степени Ax4+Bx3+Cx2+Dx+E=0»
Программа «Решение уравнения четвёртой степени Ax4+Bx3+Cx2+Dx+E=0».
Код программы «Решение уравнения четвёртой степени Ax4+Bx3+Cx2+Dx+E=0»
Вывод корней кубического уравнения.
На главную страницу.