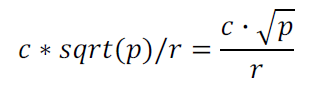Координаты проекции точки на плоскость и на прямую.
Расстояние от точки до плоскости и до прямой.
Координаты проекции точки на плоскость.
Плоскость ABC задана координатами трёх её точек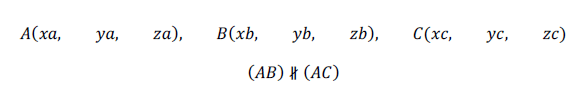
Задана точка
Точка M является проекцией точки S на плоскость ABC:
Найти координаты точки M
Координаты векторов
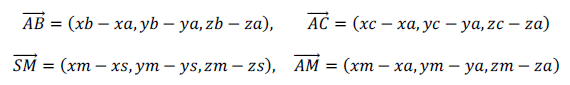
По условию, так как прямые AB и AC не параллельны, векторное произведение векторов
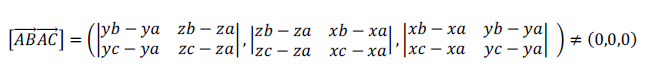
Равно нулю смешанное произведение векторов
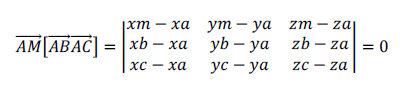
Прямая, перпендикулярная двум пересекающимся прямым, лежащим в плоскости, перпендикулярна этой плоскости
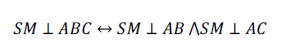
Равны нулю скалярные произведения:

Получаем систему из трёх уравнений с тремя неизвестными xm, ym, zm:
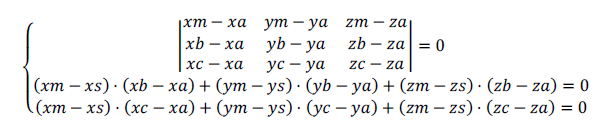
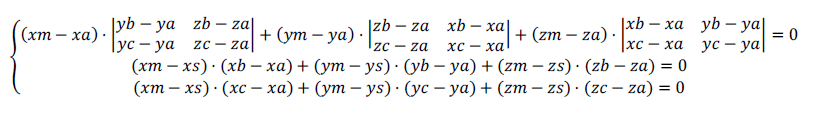
Введём обозначения
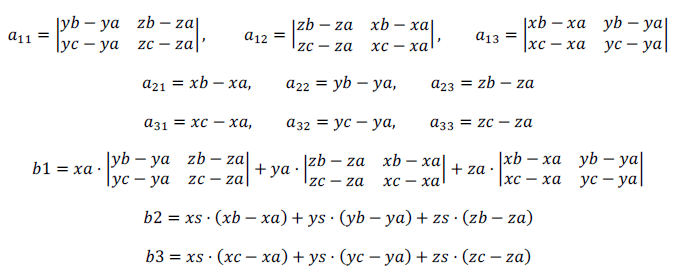
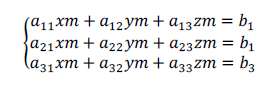
Определитель этой системы отличен от нуля:
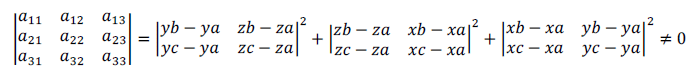
Система имеет единственное решение:
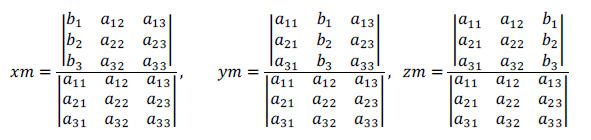
Расстояние от точки до плоскости.
Расстояние между точкой S и плоскостью ABC может быть найдено по формуле:
Расстояние между точкой S и плоскостью ABC может быть найдено вторым способом, как высота параллелепипеда, сторонами которого являются [AB] и [AC], а боковым ребром является [AS].

Векторное произведение векторов AB и AC имеет координаты:

Модуль векторного произведения векторов AB и AC:
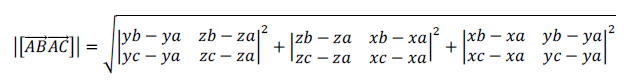
Модуль смешанного произведения векторов AS, AB, AC:
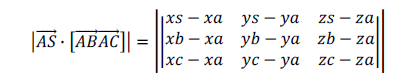
Расстояние между точкой S и плоскостью ABC может быть найдено по формуле:

Координаты проекции точки на прямую.
Прямая AB задана координатами двух её точек
Задана точка
Точка K является проекцией точки S на прямую AB.
Найти координаты точки K
Для нахождения координат точки K используем условия:
- Векторы AK и AB – коллинеарны, их координаты пропорциональны;
- Векторы SK и AB ортогональны, и их скалярное произведение равно нулю ;


Из первого уравнения
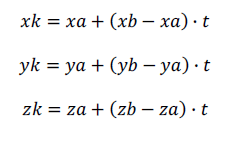
Подставляя xk, yk, zk во второе уравнение, находим t:
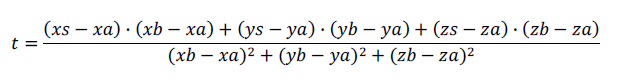
Координаты проекции точки S на прямую AB, то есть координаты точки K(xk, yk, zk):
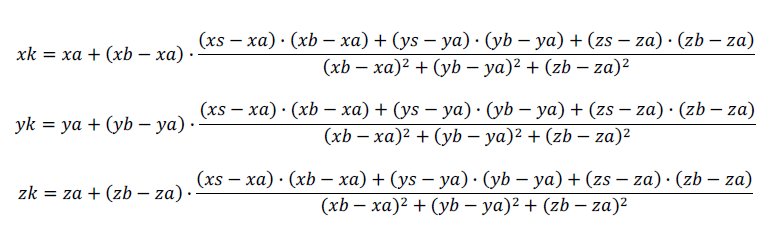
Расстояние от точки до прямой.
Расстояние между точкой S и прямой AB может быть найдено по формуле: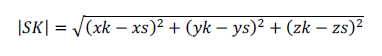
Расстояние между точкой S и прямой AB может быть найдено вторым способом, как высота параллелограмма, сторонами которого являются [AB] и [AS].

Векторное произведение векторов AB и AS имеет координаты:

Модуль векторного произведения векторов AB и AS:
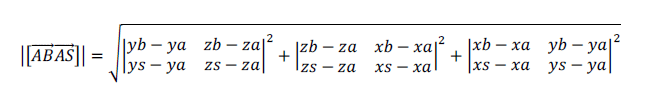
Модуль вектора AB:
Расстояние между точкой S и прямой AB может быть найдено по формуле:

Программа «Координаты проекции точки на плоскость, на прямую.
Расстояние от точки до плосоксти, до прямой».
Программа «Координаты проекции точки на плоскость, на прямую. Расстояние от точки до плосоксти, до прямой».
Версия от 15 декабря 2012 года.