Владимир Фомин. О сдаче ЕГЭ в 2011 году.
За голую акцию протеста 18 ноября 2011 года я был отчислен с третьего курса математического факультета ИВГУ. Пришлось снова задать документы на математический факультет ИВГУ. 8 июля 2011 года я сдавал ЕГЭ по русскому языку, 11 июля – по математике, 13 июля - по физике.О нерешённых задачах по математике.
Задание С4. Через вершину
правильного шестиугольника 
проведена прямая, которая делит этот шестиугольник на две части, площади которых онтносятся как 5:13, и пересекает прямую 
в точке 
. Найти отношение 
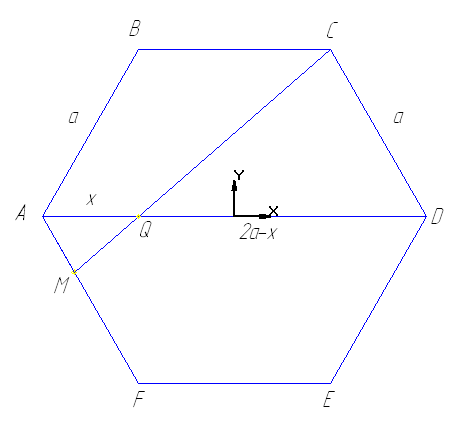
Обозначим
Тогда
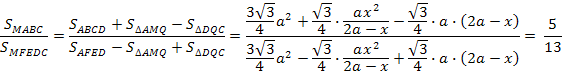
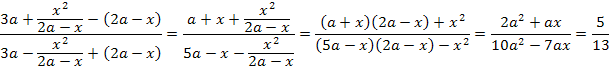
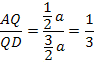
Не вполне правильный ответ, который я дал:
За этот ответ мне было начислено 2 балла из 3, так как не рассмотрен случай, когда x>a.
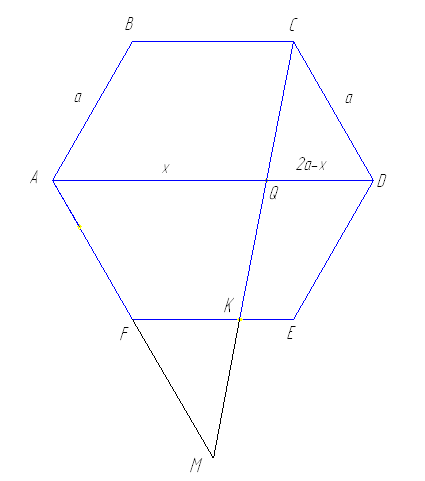
Обозначим
Тогда
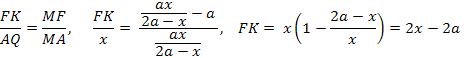
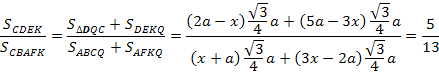
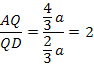
Ответ:
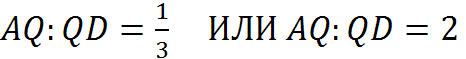
Задание С5.
Найти все значения параметра
, при которых имеет единственное решение система уравнений
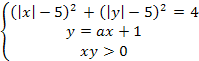
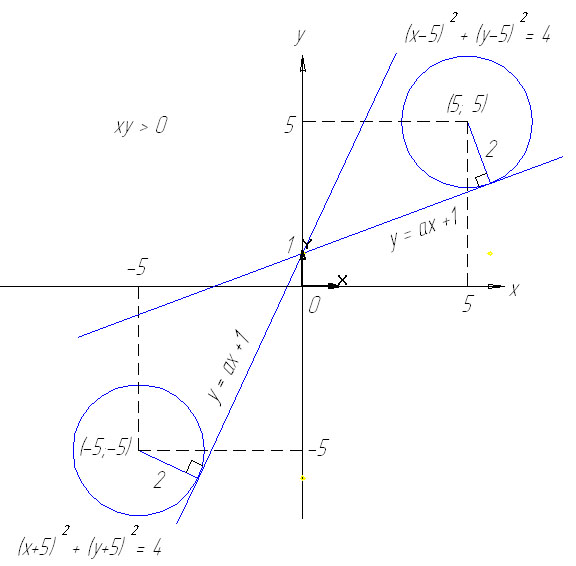
Искомое
равно тангенсу угла наклона изображённых на рисунке двух прямых.
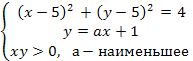или
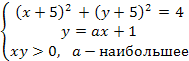
Подставляем второе уравнение систем в первое уравнение, и учитываем то, что квадратное уравнение имеет единственное решение, когда его дискриминант равен нулю.
Для первой системы получим:
Это квадратное уравнение имеет единственное решение при таких значениях параметра
, при которых его дискриминант равен нулю: 
Надо взять наименьший корень из двух полученных корней, так как вторая касательная к верхней окружности, имеющая больший угол наклона, пересечёт нижнюю окружность в двух точках, то есть система будет иметь не одно, а три решения, если
Первая система имеет единственное решение при
Для второй системы получим:
Это квадратное уравнение имеет единственное решение при таких значениях параметра
, при которых его дискриминант равен нулю: 
Надо взять наибольший корень из двух полученных корней, так как вторая касательная к нижней окружности, имеющая меньший угол наклона, пересечёт верхнюю окружность в двух точках, то есть система будет иметь не одно, а три решения, если
Вторая система имеет единственное решение при
Ответ:
По невнимательности был потерян знак при решении второй системы, в результате чего перед 30 во втором ответе стоял знак минус. За эту задачу мне зачли 2 балла из 4.
На решение задачи C6 мне не хватило времени. Поэтому результат ЕГЭ по математике был 84 балла.
На экзамене по физике одну из задач я решил не школьным методом.
Задача С4 по физике:
К батарее с ЭДС E=12 В через сопротивление R=500 Ом подключается незаряженный конденсатор ёмкостью C=0,1 мкФ. Определить тепло Q, которое выделится за время зарядки конденсатора на сопротивлении. Внутренним сопротивлением батареи и сопротивлением соединительных проводов пренебречь.
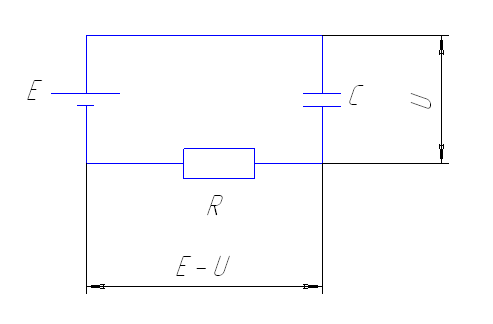
ЭДС равна сумме падений напряжений на резисторе с сопротивлением
и на конденсаторе c ёмкостью : 
Если напряжение на конденсаторе равно
, то напряжение на резисторе равно: 
Если заряд на обкладках конденсатора равен q , то из формулы
получим напряжение на конденсаторе:
Напряжение на резисторе:
Сила тока, текущего через резистор:
Сила тока является производной по времени от заряда, так как она равна заряду, проносимому в единицу времени через поперечное сечение проводника.
Мы получили дифференциальное уравнение:
или
Решение
этого уравнения должно удовлетворять условиям : 
Решение этого уравнения, удовлетворяющее данным условиям, представляет собой зависимость заряда на обкладках конденсатора от времени:
Дифференцируя заряд по времени, найдём зависимость силы тока от времени:
Зависимость силы тока, текущего через сопротивление, от времени имеет вид:
За бесконечно малый промежуток времени
на сопротивлении
выделится количество теплоты:
Количество теплоты, которое выделится сопротивлении за всё время зарядки конденсатора равно:
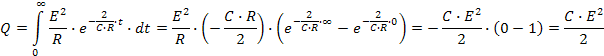
Ответ:
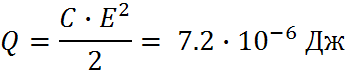
Эту задачку можно было решить и школьным методом.
Работа источника тока, совершаемая за всё время зарядки конденсатора, равна
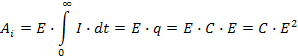
Потенциальная энергия заряженного конденсатора
Выделившееся на резисторе тепло:
Все задачи C1, C2, C3, C4, C5, C6 по физике были решены верно. Из 25 заданий части A 23 выполнены верно.
Тестовый бал - 94